A Star 알고리즘은 기본으로 Djikstra 알고리즘을 확장한 개념으로 다음 노드로 이동하는 과정에서 가중치가 가장 작은 노드를 우선으로 탐색하는 개념은 동일하다.

우선순위 큐에서 Top을 뽑을 때 djikstra는 시작부터 현재 노드까지 누적비용(g)가 가장 작은 노드를 우선으로 뽑는다. 하지만 A*는 현재까지 누적 비용(g)와 현재 부터 목적지 까지의 휴리스틱 비용(h)를 합쳐 가장 작은것을 우선으로 뽑는다.
이해를 돕자면 djikstra는 현재에 충실하는 반면, A*는 미래까지도 확인하여 탐색하는 노드 확장을 기하 급수적으로 줄일 수 있다.
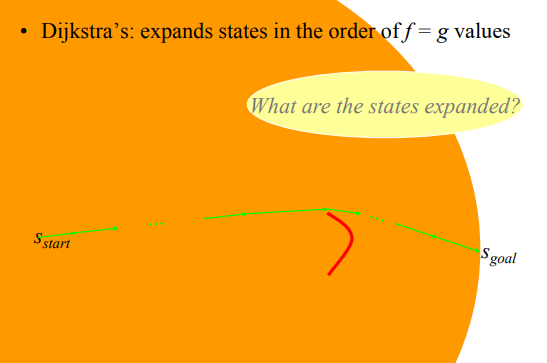
아래 그림은 (Djikstra, A*, Weighted A*)를 사용했을때 탐색 범위이다.


G 값 계산
A*의 g값을 계산하는 방법은 다양하며, 확장 방향에 따라 다르다
- 상하좌우 확장 : 현재 위치에서 상하좌우로만 확장을 한다면 g의 값은 1이 된다.
- 대각선 포함 확장 : 대각선을 포함하여 확장한다면, 상하좌우 g의 값은 기존과 동일하게 1이된다. 대각선의 경우 유클리디안 거리를 바탕으로 약 1.414가 된다.
H값 계산
A*에서 h는 휴리스틱 추정 값으로 현재 위치에서 도착지 까지의 휴리스틱 거리를 의미한다.
앞서 언급한 것처럼 A* 알고리즘은 우선순위 큐를 이용하여 f=g+h 가 가장 작은 값을 우선적으로 이동하게 된다.
f=g+h에서 g가 f에 차지하는 비중은 그렇게 크지 않다. 아래 그림을 살펴보자

start를 기준으로 대각선을 살펴보면 g값은 14로 모두 동일하나, h 값은 다르다.
이 이유는 h값이 현재 위치에서 목적지까지의 거리를 계산하기 때문이다. 위의 그림에서는 h의 계산은 맨해튼 거리를 이용하여 계산 하였다. (맨해튼 거리란 S(0,0) E(5,5)일때 d= |0-5| +|0-5|를 의미한다)
여기서 h의 값으로 맨해튼 거리를 사용할 수 있는 이유를 생각해보자.
결론적으로 말하면 목적지가 하나 이기 때문에 가능하다. 중간에 장애물이 있더라도 결국 우리는 최소비용으로 목적지에 도착하기만 하면 된다. 하지만 여기서 “휴리스틱이 항상 최선을 보장하지 않는다”라는 것을 알 수 있다. 아래 그림을 살펴보자.
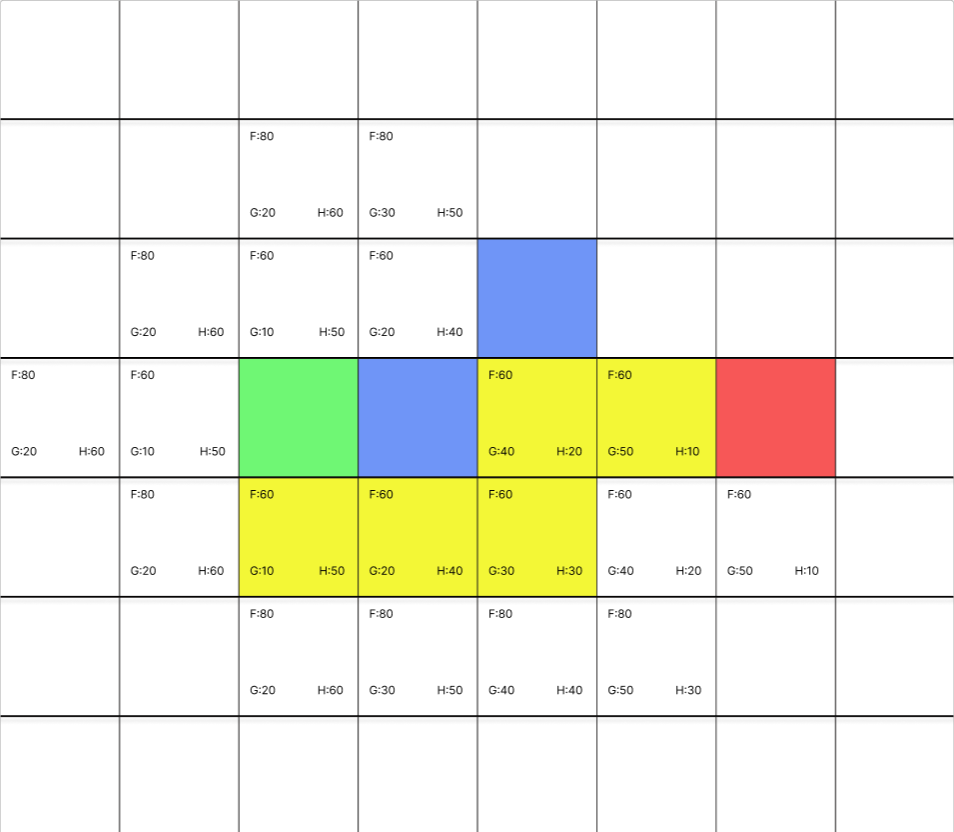
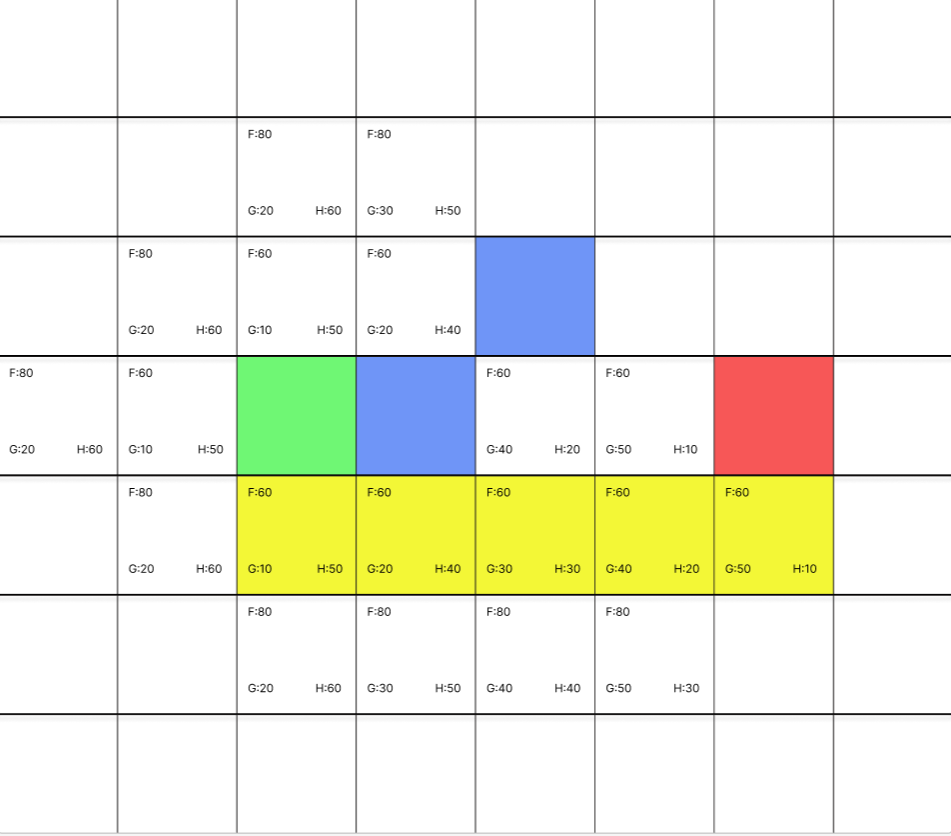

위의 그림에서 볼수 있는것 처럼 맨해튼 거리를 사용하여 경로를 구한다면 같은 F에 대해 우선순위 큐에 먼저 들어온 순서대로 이동하게 된다. 즉 위의 3개의 결과중 어떤것이 최선인지는 알수 없다.
즉 휴리스틱 값에 따라 더 많이 탐색 할수도 있고 더 적게 탐색 할 수도 있다.
이번에는 h계산을 맨해튼 거리가 아닌 유클리디안 거리로 계산한다고 가정해 보자, 맨해튼 거리에서 (0,0)에서 각각 (1,3),(2,2)는 모두 거리 4가 된다. 하지만 유클리디안 거리로 계산할 경우 각각(루트10), (루트8)이 되어 f=g+h 에서 g가 같다면 h가 더 작은 (루트8)이 조금더 최적의 경로가 될것으로 예측된다. 단, 이 경우는 목적지가 두개 이상일 경우에만 적용이 가능하다.
사실 목적지가 하나라면 h를 맨해튼 거리를 사용하나 유클리디안 거리를 사용하나 크게 차이는 없다. 하지만 목적지가 두개 이상이라면 위와 같은 상황이 발생할 수 있으므로 유클리디안 거리를 사용해야 한다.
Weighted A*
A* 알고리즘에서 다음 노드로 이동하기 위해 우선순위 사용하고 여기서 순위를 결정짓는 것은 f=g+h로 결국 f값이 작은것 부터 우리는 탐색을 하게된다.
f를 결정짓는 g와h를 살펴보면 g는 시작점부터 현재 노드까지 얼만큼 이동했는지 이동량을 나타낸다. 이는 노드 확장을 4방위(상하좌우)로 하였을 경우 맨해튼 거리로 이동하는 것과 동일해지고 변화량이 크게 바뀌지 않는다. 물론 대각선을 포함하였을 경우 유클리디안 거리로 계산 되기 때문에 약간의 변화량은 있지만 이것 또한 크게 바뀌지 않는다. (예를들어 좌- 좌상-좌상, 좌-우상-좌상 … 등으로 이동할때 g의 값은 동일하다.)
그렇다면 결국 h가 노드 확장에 큰 영향을 미치는 것을 알 수 있다. Weighted A* 알고리즘은 h값에 가중치w를 곱하여 불필요한 확장을 제거하는 역할을 한다. 이때 f= g+wh가 되고 w>1인 자연수가 된다.
어떻게 불필요한 확장을 제거할 수 있을까?
예를 들어 현재 f=60, g=10, h=12라고 가정하자. 현재 위치에서 4방향(상하좌우)로 확장 한다고 할때 확장 할 위치에서 우리는 목적지 까지 h를 유클리디안 거리 방식으로 다시 계산한다.
이때 만약 가중치w를 도입하여 1.5의 약 50% 가중치를 추가하였다고 가정하면, 상대적으로 목적지와 가까운 노드는 증가비율이 상대적으로 목적지와 먼 노드의 증가비율 보다 적게 증가할 것이다.
이는 f의 중복을 제거하게 하여 불필요한 확장을 막을 수 있다.
A* VS Weighted A*
지금부터는 A*알고리즘과 Weighted A* 알고리즘을 사용했을때 경로를 탐색하는데에 걸리는 시간을 측정해본다.
아래 코드는 Weighted A*를 구현한 코드이다.
import java.util.*
import kotlin.math.abs
import kotlin.math.sqrt
import kotlin.time.ExperimentalTime
import kotlin.time.measureTimedValue
data class Node(
val x: Int,
val y: Int,
var fCost: Double = Double.MAX_VALUE,
var gCost: Double = Double.MAX_VALUE,
var parent: Node? = null
) {
override fun equals(other: Any?): Boolean {
if (other == null || other !is Node) {
return false
}
return x == other.x && y == other.y
}
override fun hashCode(): Int {
return Objects.hash(x, y)
}
}
fun getDistance(node1: Node, node2: Node): Double {
val dx = abs(node1.x - node2.x)
val dy = abs(node1.y - node2.y)
return sqrt((dx * dx + dy * dy).toDouble())
}
fun reconstructPath(current: Node): List<Node> {
val path = mutableListOf<Node>()
var node: Node? = current
while (node != null) {
path.add(node)
node = node.parent
}
return path.reversed()
}
fun weightedAStar(
start: Node,
goal: Node,
grid: Array<Array<Double>>,
weight: Double,
visited: Set<Node> = setOf()
): List<Node> {
val openSet = PriorityQueue<Node>(compareBy { it.fCost })
val closedSet = mutableSetOf<Node>()
start.gCost = 0.0
start.fCost = getDistance(start, goal) * weight
openSet.add(start)
while (openSet.isNotEmpty()) {
val current = openSet.poll()
if (current == goal) {
visited.plus(current)
return reconstructPath(current)
}
closedSet.add(current)
val neighbors = mutableListOf<Node>()
val dx = intArrayOf(-1, 0, 1, 0)
val dy = intArrayOf(0, -1, 0, 1)
for (i in dx.indices) {
val neighbor = Node(current.x + dx[i], current.y + dy[i])
if (neighbor.x !in grid.indices || neighbor.y !in grid[0].indices) {
continue
}
if (visited.contains(neighbor)) {
continue
}
if (grid[neighbor.x][neighbor.y] == 0.0) {
neighbors.add(neighbor)
}
}
for (neighbor in neighbors) {
val tentativeGCost = current.gCost + getDistance(current, neighbor)
if (tentativeGCost < neighbor.gCost) {
neighbor.parent = current
neighbor.gCost = tentativeGCost
neighbor.fCost = neighbor.gCost + getDistance(neighbor, goal) * weight
if (neighbor !in openSet) {
openSet.add(neighbor)
}
}
}
}
return emptyList()
}참고로 w의 값을 1로 설정하면 일반 A* 알고리즘으로 동작한다.
- A* 알고리즘 수행 시간
val measuredTime = measureTimedValue {
val path1 = weightedAStar(start, passThrough.first(), grid, 1.0, visited)
val path2 = weightedAStar(passThrough.first(), passThrough.last(), grid, 1.0, visited)
val path3 = weightedAStar(passThrough.last(), goal, grid, 1.0, visited)
val path = path1 + path2.drop(1) + path3.drop(1)
// Print the result
if (path.isNotEmpty()) {
for (node in path) {
println("(${node.x}, ${node.y})")
}
} else {
println("No path found.")
}
}
//result => kotlin.Unit || measured time ==>764.208500ms- Weighted A* 알고리즘 수행시간
val measuredTime = measureTimedValue {
val path1 = weightedAStar(start, passThrough.first(), grid, 1.5, visited)
val path2 = weightedAStar(passThrough.first(), passThrough.last(), grid, 1.5, visited)
val path3 = weightedAStar(passThrough.last(), goal, grid, 1.5, visited)
val path = path1 + path2.drop(1) + path3.drop(1)
// Print the result
if (path.isNotEmpty()) {
for (node in path) {
println("(${node.x}, ${node.y})")
}
} else {
println("No path found.")
}
}
//result => kotlin.Unit || measured time ==>85.328600ms위의 결과에서 확인 할수 있듯이 w값을 설정하였을 경우 탐색 속도가 빨라지는 것을 알 수 있다.
하지만 그렇다고 해서 w값을 터무니 없이 크게 설정하면 제대로 된 결과를 얻을 수 없다.
'Dev' 카테고리의 다른 글
| Spring Boot 3.0.X에 Kotlin JDSL 적용하기 (0) | 2023.04.19 |
|---|---|
| 그리드 분할을 이용한 Weighted A* 성능 최적화 (0) | 2023.04.01 |
| IntelliJ 한글 깨짐 원인 & 해결 (0) | 2023.03.11 |
| OOME(Out Of Memory Error) 발생 및 해결 (0) | 2022.11.30 |
| XML vs JSON vs YAML (0) | 2022.02.07 |