안녕하세요. 오랜만에 문어체로 시작하는데요, 학부동안 배운 알고리즘 또는 배우지 못한 다양한 알고리즘 및 자료구조 이론을 정리해보려고 합니다. 설명 과정에 틀린 부분이나 추가해야할 부분이 있으면 언제든지 답글 달아주시면 감사하겠습니다.
오늘 배워볼 알고리즘은 KMP 알고리즘입니다. 문자 검색을 하는 가장 기본적인 방법은 부르트포스 방법으로 순차적으로 패턴을 비교하는 방법이지만 이 방법으로하면 패턴(M)이 길어지거나 문자(N)가 길어진다면 O(NM)의 시간복잡도를 가지게 됩니다. (여기서는 부르트포스 방법은 설명하지 않겠습니다.)
KMP (Knuth Morris Partt Algorithm)
앞서 언급했듯이 부르트포스 방법으로 구현한다면 시간 복잡도는 O(NM)입니다. KMP 알고리즘은 부르트포스 알고리즘에서 불필요한 부분은 건너뛰고 비교가 필요한 부분만 비교함으로써 성능을 개선시키는 알고리즘 입니다. KMP 알고리즘의 시간 복잡도는 O(N+M)이 됩니다. 하지만 패턴에 반복이 없으면 효율이 않좋아지게 됩니다.
그렇다면 어떻게 불필요한 부분을 건너 뛰는지 알아보도록 하겠습니다.(사용되는 용어는 2가지로 접두부, 접미부입니다.)
- 제일 먼저 탐색 문자열에 대해 스킵테이블을 구해 놓아야 합니다.
- 스킵테이블이란 탐색 문자열의 부분 문자열 중 접두부와 접미부가 있고 이 둘이 서로 같을때 얼만큼 스킵할 수 있는지 나타내는 테이블 입니다.
- 하지만 이 테이블을 구성하는것 또한 부르트포스 방법으로 구한다면 시간복잡도가 O(M^2)이 됩니다. 따라서 KMP 알고리즘을 이용하여 스킵 테이블을 구해야 합니다.
- KMP를 위해 두개의 변수가 필요합니다.
- 하나는 begin으로 원본 문자열의 탐색 시작 위치가 됩니다.
- 나머지 하나는 matched로 비교를 시작할 위치를 나타냅니다.
1. GetSkipTable(스킵테이블)
vector<int> getSkipTable(string pattern)
{
int p = pattern.size();
vector<int> skipTable(p, 0);
int begin = 1, matched = 0; // matched는 몇개가 맞는지 length를 나타낸다.
while(begin + matched < p)
{
if(pattern[matched] == pattern[begin + matched]) // matched는 접두부,begin+matched는 접미부를 나타낸다.
{
matched++;
skipTable[begin + matched - 1] = matched;
}
else
{
if(matched == 0)
{
begin++;
}
else
{
// KMP 문자열 탐색 알고리즘 과 동일하게 불일치 발생 시
// 매칭을 진행하면서 구했던 접두 접미사 길이 만큼 탐색을 건너뛸 수 있다
begin += matched - skipTable[matched - 1];
matched = skipTable[matched - 1];
}
}
}
return skipTable;
}위의 코드는 스킵테이블을 KMP를 이용하여 구하는 방법입니다. 간략한 설명은 주석으로 달아놨습니다. 아래 그림은 패턴을 넣었을때 생성된 스킵테이블 결과입니다. 간단히 설명하자면 특정 패턴의 부분 문자열 중 접두부와 접미부를 비교하여 일치하는 부분 문자열의 길이를 저장한 테이블 입니다. 이 테이블이 필요한 이유는 아래에서 자세하게 설명하겠습니다.

2. KMPSearch
그럼 이제 원본 문자열에서 탐색 문자열이 일치하는 곳이 있는지 없는지 찾아보고, 있다면 시작 위치를 반환하는 KMP를 구현해 보겠습니다. 아래 그림은 KMP를 어떻게 구현해야 하는지 간단한 그림으로 표현한 것입니다.
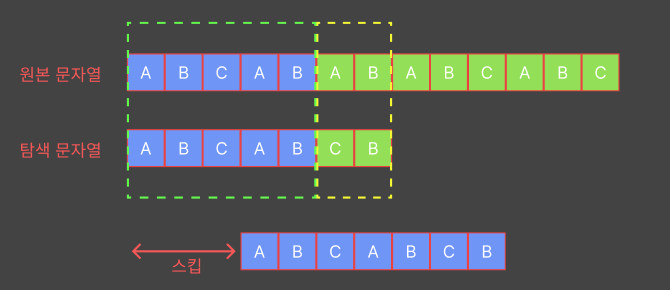
처음 begin과 Matched는 모두 0으로 초기화를 해주고 (원본 문자열 길이 - 탐색 문자열 길이) 만큼 반복을 해줍니다. 이 과정에서 우리는 스킵테이블을 이용하여 비교횟수를 줄여줄 예정입니다.
vector<int> kmpSearch(string s, string pattern)
{
vector<int> ret;
vector<int> skip_table;
int originLength = s.size(), patternLength = pattern.size();
int begin = 0, matched = 0; // begin: 원본 문자열 탐색 시작 위치, matched: 비교를 시작할 위치
skip_table = getSkipTable(pattern); // 위에서 구현한 스킵테이블 저장
//원본 문자열의 시작위치가 범위를 벗어나기 전까지 반복
while(begin <= originLength - patternLength)
{
// 비교위치가 패턴 길이를 넘지 않으면서 원본 문자열과 탐색 문자열을 비교해준다.
// 이를 통해 탐색 문자열의 어디까지가 원본 문자열과 일치하는지 알 수 있다.
if(matched < patternLength && s[begin + matched] == pattern[matched])
{
matched++;
// 패턴과 일치하다면 그 때의 원본 문자열에서 탐색 시작 위치를 저장한다.
if(matched == patternLength)
{
ret.push_back(begin);
}
}
else
{
//비교 위치가 0이라면 탐색 위치를 증가시켜준다.
//이는 접두부, 접미부는 최소 크기가 2 이상인 문자열 일때 표현이 가능하기 때문이다.
if(matched == 0)
{
begin++;
}
else //0이 아니라면 스킵테이블을 확인하여 차이만큼 원본 문자열의 탐색 위치를 스킵을 해주고, 비교 위치를 스킵테이블을 이용하여 조정해준다.
{
begin += matched - skip_table[matched - 1];
matched = skip_table[matched - 1];
}
}
}
return ret;
}위의 코드는 KMP 구현 부분입니다. 설명 편의상 탐색 문자열을 패턴이라고 쓰도록 하겠습니다.
위의 그림을 살펴보면 초록색 점선과 노란색 점선이 있고 이는 각각 문자열이 일치하는 부분과 일치하지 않은 부분입니다. 이제 가장 중요한 스킵하는 부분을 설명하겠습니다.
위의 그림 상황에서 begin과 matched를 확인해 본다면 각각 begin = 0, matched = 5 가 되고,
코드 상의 if(matched < patternLength && s[begin + matched] == pattern[matched]) 를 대입해 보면 해당 위치에서 원본 문자열의 값은 "A" 이지만, 탐색 문자열은 "C"인것을 확인할 수 있습니다. 이 상황에서 우리가 짐작할 수 있는것은 현재 시작 위치(begin)에서 일치하는 패턴을 찾을수 없다는 것입니다. 그럼 다음 패턴의 시작점은 어떻게 찾을까요?
스킵테이블을 이용하여 begin의 시작점을 스킵해 봅시다.
그림을 보면 현재 matched - 1 까지는 일치하는 것을 알 수 있습니다. 그러면 일치하는 부분에서 얼마큼 스킵을 할수 있을까요? 방법은 우리가 아까 구해놓은 스킵테이블을 이용하면 쉽게 구할 수 있습니다.
코드 내에 begin += matched - skip_table[matched - 1]; 이 부분을 보면 현재 일치하는 패턴 길이에서 해당 패턴이 스킵테이블에서 얼만큼 접두부와 접미부가 일치하는지 길이를 빼주면 스킵할 수 있는 길이가 나옵니다.
스킵테이블 결과 그림을 보면 idx 4 가 ABCAB 에서 접두부와 접미부 가 같은 AB의 길이를 저장하고 있습니다. 따라서 전체길이 5에서 일치하는 패턴 길이 2를 빼주면 3만큼 스킵이 가능합니다.
다음은 matched를 조정해주어야 합니다. 현재 matched는 5이지만 스킵을 한 후에는 일치하는 부분의 길이가 2로 줄어들게 됩니다. 여기서 2는 스킵테이블에서 바로 구할 수 있습니다.
이것으로 KMP 알고리즘 설명을 마치겠습니다.
처음 알고리즘을 이해하는데 그래서 이게 왜 동작하지?? 라는 생각이 들었는데 자세히 내용을 따라가다 보니 왜 스킵테이블이 필요한지, 스킵테이블을 구하기 위해 왜 KMP 알고리즘이 쓰이는지 알수 있었습니다.
다른 분들이 작성한 블로그를 보면 제가 풀이한 방식 말고 다른 방식으로 풀이한 분들이 계신것 같습니다. 제 풀이가 무조건 정답은 아니기 때문에 KMP 알고리즘이 어떤 방식으로 동작하는지만 이해하고 넘어가주시면 감사하겠습니다.